Physics Harmonic Pathways: Smooth Interaction Flows
Welcome to Harmonic Pathways, where we explore how systems within the Unison lattice create harmonic flows of energy, influence, and data. These flows result in smooth, predictable patterns of interaction across the network.
Unison Heartbeat: Finding Harmony in Resistance
The unison heartbeat is the temporal rhythm of the MiCi system, aligning spatial and scalar nodes to achieve dynamic harmony. Resistance, or the energy cost of coordination, decreases when waveforms from scalar nodes interact constructively.
Constructive Interference and Harmony
- Waveform Alignment: Scalar waveforms align, amplifying their combined effects and reducing resistance.
- Energy Optimization: Constructive interference minimizes energy loss, maximizing system efficiency.
- Mathematical Framework: Resistance \( R \) decreases as waveforms synchronize, creating a self-sustaining rhythm.
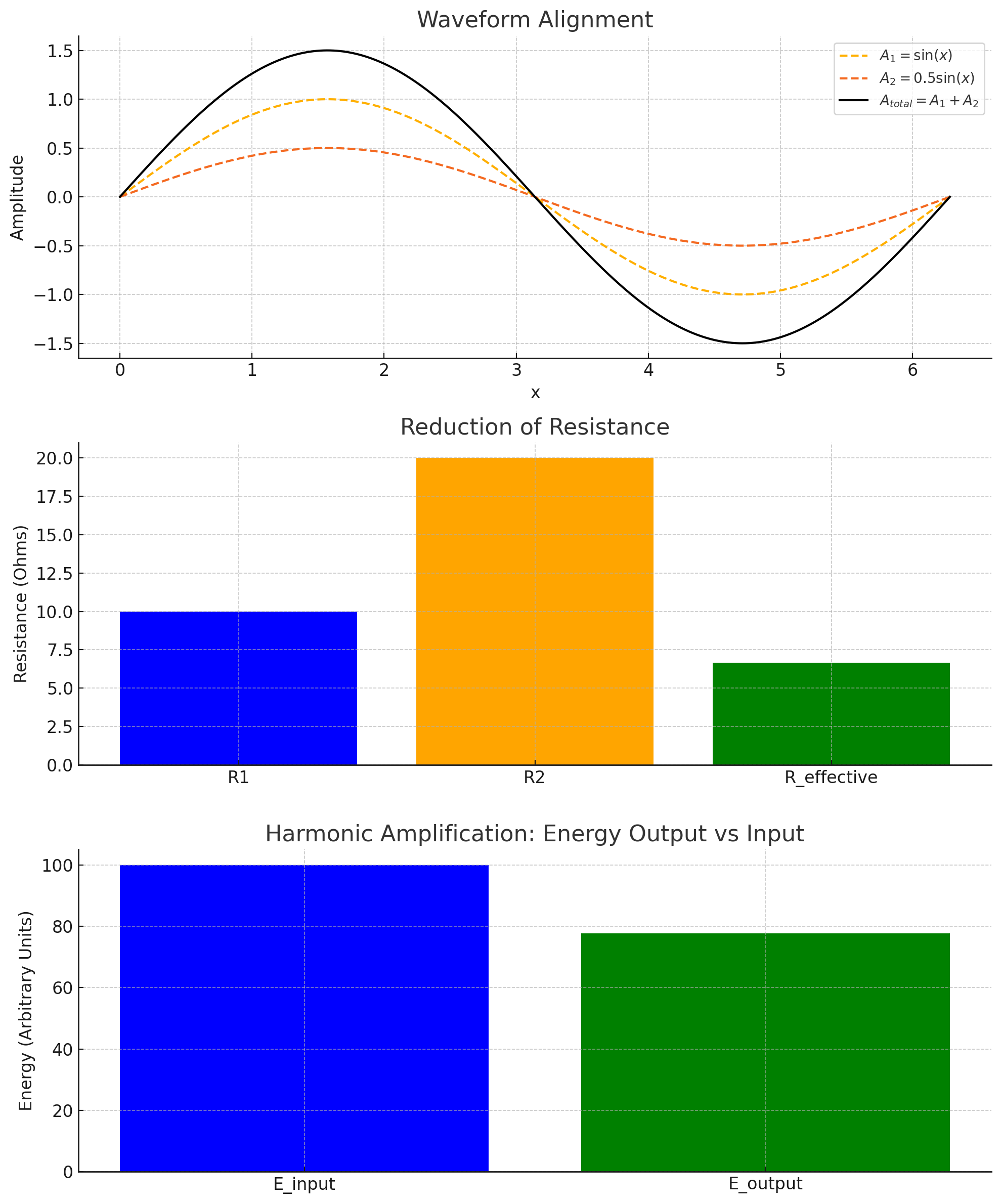
“Harmony is achieved when the unison heartbeat resonates through the system, aligning scalar nodes with constructive precision.”
How Harmonic Pathways Form
Harmonic pathways form when nodes and systems within the lattice reach a state of resonance or balance. Aligned forces, data, or fields create a harmonic flow where interactions are synchronized, and energy is evenly distributed.
Key Factors in Pathway Formation
- Resonance: Alignment of frequencies or forces between nodes.
- Synchronization: Perfectly timed interactions, ensuring minimal resistance.
- Energy Distribution: Even energy spread, preventing overloading or underutilization.
The Role of Harmonics in System Efficiency
Harmonic pathways are essential for optimizing system efficiency. When systems operate in harmony:
- Energy Conservation: Minimized energy loss along paths of least resistance.
- Optimized Data Flow: Faster, more accurate data transmission reduces bottlenecks.
- System Stability: Balanced pathways prevent overloads and ensure resilience to fluctuations.
Applications of Harmonic Pathways in MiCi
Harmonic pathways have a wide range of applications in the MiCi framework:
- Signal Processing: Reliable, interference-free communication.
- Energy Grids: Efficient energy distribution across complex systems.
- Machine Learning: Enhanced pattern recognition and adaptability.
- Resource Allocation: Balanced resource distribution prevents overloads.
Harmonic Pathways and the MiCi Framework
In the MiCi framework, harmonic pathways represent the ultimate state of efficiency. These pathways act as the backbone of the Unison lattice, guiding energy, data, and influence along the most efficient routes.
What's Possible?
Unison Lattice, communication arrays, directional energy routers, and intercepts of holographic map distributed through 3D (Volume) Spatial Processors.
Unison Lattice